今回はTensorFlowのチュートリアルの回帰(Regression)をやってみます。
このチュートリアルでは、1970年代後半と1980年代初頭の自動車の燃費を予測するためのモデルを構築します。自動車のモデルにはシリンダーや排気量、馬力、重さのような属性があります。
動作環境
python3.6, tensorflow 1.12.0
では実装に行きましょう!
モジュールのインポート
seabornというペアプロット図を描画するためのモジュールをインストールします。
私の場合はpandasもインストールしました。
pip install seaborn pip install pandas
モジュールをインポートします。テンソルフローのバージョンは1.12.0です。
from __future__ import absolute_import, division, print_function import pathlib import pandas as pd import seaborn as sns import tensorflow as tf from tensorflow import keras from tensorflow.keras import layers
Auto MPG データセット
MPGというのはmiles per gallonの意味で1ガロン当たりの走行距離(マイル)を表します。日本でいうkm/Lと同様です。
データを取得する
データセットをダウンロードします。
dataset_path = keras.utils.get_file("auto-mpg.data", "https://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data")
dataset_path
【結果】ダウンロードログが表示されます。——にはuser名が入ります。
Downloading data from https://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data 32768/30286 [================================] - 0s 7us/step '/Users/------/.keras/datasets/auto-mpg.data'
このデータをpandasを使ってインポートします
column_names = ['MPG','Cylinders','Displacement','Horsepower','Weight',
'Acceleration', 'Model Year', 'Origin']
raw_dataset = pd.read_csv(dataset_path, names=column_names,
na_values = "?", comment='\t',
sep=" ", skipinitialspace=True)
dataset = raw_dataset.copy()
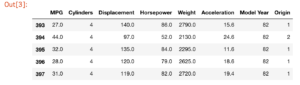
dataset.tail()
【結果】データセットの最後の5つが表示されます。
データを消去する
このデータセットには未知数が含まれているデータがあります。実装を簡単にするためにこれらのデータを消去します。isna()メソッドで未知数のデータか判定しています。
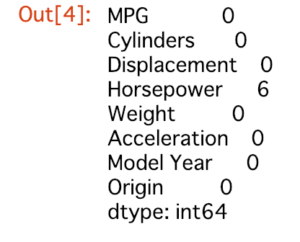
dataset.isna().sum()
【結果】Horsepowerに6つ未知数のデータが含まれているようです。
データから消去します。
dataset = dataset.dropna()
Originは数値ではなく、実際のカテゴリーです。そのため、このデータをワン・ホットに変換します。
ワン・ホットとは一つだけ1で他は0であるビット列です。ここでは、USA, Europe, Japanの分類を各配列に分けて当てはまる分類を1, それ以外を0にしています。
origin = dataset.pop('Origin')
dataset['USA'] = (origin == 1)*1.0
dataset['Europe'] = (origin == 2)*1.0
dataset['Japan'] = (origin == 3)*1.0
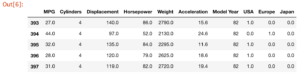
dataset.tail()
【結果】変換結果の最後のデータを5件表示しています。
各行で、USA, Europe, Japanのどれか1つが1.0, それ以外が0.0であることが分かります。
訓練データとテストデータ
データを訓練データとテストデータに分けます。テストデータは出力されたモデルの評価に使います。
train_dataset = dataset.sample(frac=0.8,random_state=0) #80%のデータを訓練用データとする test_dataset = dataset.drop(train_dataset.index) # 訓練用データ以外のデータをテストデータとする
データを検査する
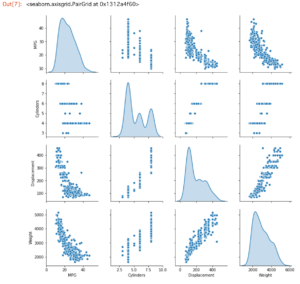
訓練用データからいくつかのカラムのペアの同時分布を表示してみます。
sns.pairplot(train_dataset[["MPG", "Cylinders", "Displacement", "Weight"]], diag_kind="kde")
【結果】
包括的な統計も表示もしてみます。
train_stats = train_dataset.describe()
train_stats.pop("MPG")
train_stats = train_stats.transpose()
train_stats
【結果】
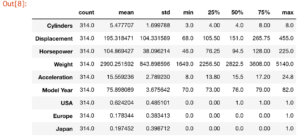
ラベルから特徴を分割します。目標値-“ラベル”を特徴から分離します。このラベルは訓練させたモデルが予測できるようになるためのラベルです。
データを正規化する
先ほど表示した訓練用データの統計を見ると各特徴の範囲が異なることが分かります。各特徴の値の範囲が違うと訓練が難しくなるためデータを正規化すべきです。
正規化するためのメソッドを定義して、訓練データとテストデータを正規化します。
正規化は
(データの値 – 平均値) ÷ 標準偏差
で行なっています。
def norm(x): return (x - train_stats['mean']) / train_stats['std'] normed_train_data = norm(train_dataset) normed_test_data = norm(test_dataset)
モデルを操作する
モデルの構築
2つの密結合した隠れ層と、単一で連続値を返す出力層からなるモデルを使います。
後に2つ目のモデルを作るため、モデルを構築するステップをまとめたbuild_modelメソッドを作ります。
損失関数に平均二乗誤差(MSE)を、評価関数に平均絶対誤差と平均二乗誤差を、オプティマイザにRMSPropOptimizerを指定しています。
def build_model():
model = keras.Sequential([
layers.Dense(64, activation=tf.nn.relu, input_shape=[len(train_dataset.keys())]),
layers.Dense(64, activation=tf.nn.relu),
layers.Dense(1)
])
optimizer = tf.train.RMSPropOptimizer(0.001)
model.compile(loss='mse',
optimizer=optimizer,
metrics=['mae', 'mse'])
return model
model = build_model() # 構築したモデルを変数に代入します
モデルの検査
.summaryメソッドを使うとモデルの簡単な説明が表示されます。
model.summary()
【結果】

訓練データから10個データを取り出し、example_batchとします。これを引数としてmodel.predictメソッドを呼びます。
example_batch = normed_train_data[:10] example_result = model.predict(example_batch) example_result
【結果】期待される形や種類を出力するモデルを作り出せそうなデータが取得できました。

モデルを訓練する
エポックを1000としてモデルを訓練します。そして、history変数にトレーニングやバリデーションの正確性を記録します。
# Display training progress by printing a single dot for each completed epoch
class PrintDot(keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs):
if epoch % 100 == 0: print('')
print('.', end='')
EPOCHS = 1000
history = model.fit(
normed_train_data, train_labels,
epochs=EPOCHS, validation_split = 0.2, verbose=0,
callbacks=[PrintDot()])
【結果】モデルを1回訓練するごとにドットが出力されます。
history変数から、トレーニングの経過を可視化します。
hist = pd.DataFrame(history.history) hist['epoch'] = history.epoch hist.tail()
【結果】最後の5回の訓練結果が表示されました。
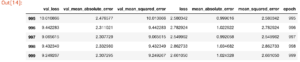
グラフで表示できるように関数を定義して表示します。
import matplotlib.pyplot as plt
def plot_history(history):
plt.figure()
plt.xlabel('Epoch')
plt.ylabel('Mean Abs Error [MPG]')
plt.plot(hist['epoch'], hist['mean_absolute_error'],
label='Train Error')
plt.plot(hist['epoch'], hist['val_mean_absolute_error'],
label = 'Val Error')
plt.legend()
plt.ylim([0,5])
plt.figure()
plt.xlabel('Epoch')
plt.ylabel('Mean Square Error [$MPG^2$]')
plt.plot(hist['epoch'], hist['mean_squared_error'],
label='Train Error')
plt.plot(hist['epoch'], hist['val_mean_squared_error'],
label = 'Val Error')
plt.legend()
plt.ylim([0,20])
plot_history(history)
【結果】
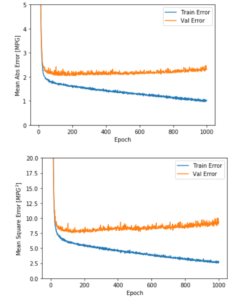
このグラフからモデルが多少改善したが、数百回のエポック後は検証エラーの劣化もみられます。検証スコアが向上しない場合は、自動的に訓練を停止するようにメソッドを更新します。
エポックごとに訓練条件をテストとするコールバックを使用します。
先ほどとの違いはearly_stop変数にテストするための条件をセットし、callbacks変数に追加しています。
model = build_model()
#patience値は改善をチェックするためのエポックの数です
#
early_stop = keras.callbacks.EarlyStopping(monitor='val_loss', patience=50)
history = model.fit(normed_train_data, train_labels, epochs=EPOCHS,
validation_split = 0.2, verbose=0, callbacks=[early_stop, PrintDot()])
plot_history(history)
【結果】ドットが先ほどより少なくなりました。途中で訓練を中止したことが分かります。
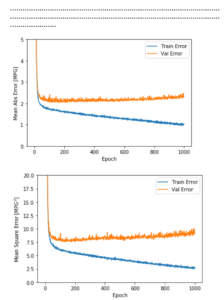
このグラフはバリデーションセットでは平均誤差が+/- 2MPG前後であることを示しています。次にテストデータを使ってモデルのパフォーマンスをみます。
loss, mae, mse = model.evaluate(normed_test_data, test_labels, verbose=0)
print("Testing set Mean Abs Error: {:5.2f} MPG".format(mae))
【結果】テストセットによる平均誤差が1.96 MPGと出ました。
Testing set Mean Abs Error: 1.96 MPG
予測する
最後にテストデータを使ってMPG値を予測します。
test_predictions = model.predict(normed_test_data).flatten()
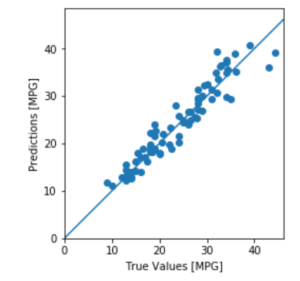
plt.scatter(test_labels, test_predictions)
plt.xlabel('True Values [MPG]')
plt.ylabel('Predictions [MPG]')
plt.axis('equal')
plt.axis('square')
plt.xlim([0,plt.xlim()[1]])
plt.ylim([0,plt.ylim()[1]])
_ = plt.plot([-100, 100], [-100, 100])
【結果】直線に近い点ほど正しく予測できています。
error = test_predictions - test_labels
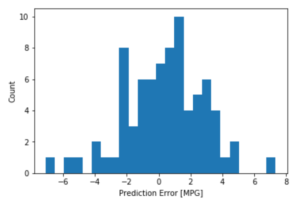
plt.hist(error, bins = 25)
plt.xlabel("Prediction Error [MPG]")
_ = plt.ylabel("Count")
【結果】MPGの予測誤差の分布が表示されました。
結論
今回は回帰問題を扱うための技術を紹介しました。
- 平均二乗誤差(MSE)は回帰問題に使用される一般的な損失関数です(分類問題と異なる)
- 一般的に回帰測定に用いられる評価指標は平均絶対誤差(MAE)です。
- 入力データの各要素の値の範囲が異なる場合は個別に調整する必要があります。
- 訓練データが多くない場合は、過剰適合を避けるために隠れ層が少ない小規模なネットワークが好まれます。
- 学習を中断させることは過剰適用を防ぐ有効な手法です。









コメントを残す