TensorFlow チュートリアルをやってよう！　オーバーフィットとアンダーフィット編

戦略

重み正規化を追加

“オッカムの剃刀”を知っていますか？オッカムの剃刀とは、

「ある事柄を説明するためには、必要以上に多くを仮定するべきでない」

とする指針です。これはニューラルネットワークで学習されたモデルにも当てはまります。

トレーニングデータやネットワークの構造は、データを表現する複数の重みのセット（複数のモデル）であり、”単純なモデル”は”複雑なモデル”よりも過剰適合しにくいです。

ここで言う”単純なモデル”とはパラメーターの分布のエントロピーが少ないモデル（またはパラメーターの少ないモデル）です。すなわち、過剰適合を軽減する一般的な方法は、ネットワークの重みを小さい値に制限することです。

これにより重みの分布がより”規則的”になります。これは”重み正則化”と呼ばれ、ネットワークの損失関数に大きな重みに関連するコストを与えることで実装できます。

このコストには２種類あります。

L1正則化：重みの絶対値の総和に比例してコストが増加する（重みに関する”L1ノルム”と呼ばれます）

L2正則化：重みの２乗に比例してコストが増加する（重みに関する”L2ノルム”と呼ばれます）

tf.kerasで重み正則化は、重み正則化のインスタンスをキーワード引数としてレイヤに渡すことで追加できます。以下ではL2重み正則化を加えます。

l2_model = keras.models.Sequential([
    keras.layers.Dense(16, kernel_regularizer=keras.regularizers.l2(0.001),
                       activation=tf.nn.relu, input_shape=(NUM_WORDS,)),
    keras.layers.Dense(16, kernel_regularizer=keras.regularizers.l2(0.001),
                       activation=tf.nn.relu),
    keras.layers.Dense(1, activation=tf.nn.sigmoid)
])

l2_model.compile(optimizer='adam',
                 loss='binary_crossentropy',
                 metrics=['accuracy', 'binary_crossentropy'])

l2_model_history = l2_model.fit(train_data, train_labels,
                                epochs=20,
                                batch_size=512,
                                validation_data=(test_data, test_labels),
                                verbose=2)

【結果】

Train on 25000 samples, validate on 25000 samples
Epoch 1/20
 - 10s - loss: 0.5295 - acc: 0.8009 - binary_crossentropy: 0.4897 - val_loss: 0.3816 - val_acc: 0.8728 - val_binary_crossentropy: 0.3403
Epoch 2/20
 - 8s - loss: 0.3059 - acc: 0.9079 - binary_crossentropy: 0.2603 - val_loss: 0.3343 - val_acc: 0.8873 - val_binary_crossentropy: 0.2856

＜中略＞

Epoch 19/20
 - 6s - loss: 0.1507 - acc: 0.9716 - binary_crossentropy: 0.0827 - val_loss: 0.5337 - val_acc: 0.8580 - val_binary_crossentropy: 0.4654
Epoch 20/20
 - 8s - loss: 0.1480 - acc: 0.9742 - binary_crossentropy: 0.0794 - val_loss: 0.5458 - val_acc: 0.8546 - val_binary_crossentropy: 0.4771

l2(0.001)は、レイヤーにある全ての重みマトリックス係数が、ネットワークの総損失に0.001*weight_coefficient_value**2を追加することを意味します。

このペナルティーは訓練中にのみ追加されるので、ネットワークの損失はテスト時よりも訓練時の方がより大きくなります。

以下がL2正則化ペナルティーの影響です。

plot_history([('baseline', baseline_history), ('l2', l2_model_history)])

【結果】

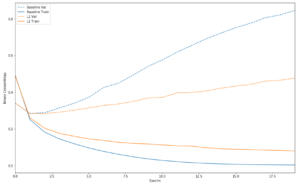
グラフから、L2正則化モデルはベースラインモデルよりも過剰適合に対する耐性がはるかに高くなっていることがわかります。両方のモデルは同じパラメーター数を持っています。

ドロップアウトを追加

ドロップアウトも一般的な正則化の方法の１つです。

ドロップアウトとは訓練中にレイヤーのノードのいくつかをランダムに０に設定することです。

0にする割合のことを”ドロップアウト率”と言います。通常は0.2~0.5が使われます。

テスト時にはノードはドロップアウトされず、代わりに出力値がドロップアウトレートに等しい係数で縮小されます。

tf.kerasではDropoutレイヤーを使ってネットワークに導入します。このレイヤーは出力するレイヤーの直前に適用されます。

IMDBネットワークにドロップアウトレイヤーを２つ追加して、過剰適合を減らすのにどれだけ効果があるかを確認しましょう。

dpt_model = keras.models.Sequential([
    keras.layers.Dense(16, activation=tf.nn.relu, input_shape=(NUM_WORDS,)),
    keras.layers.Dropout(0.5),
    keras.layers.Dense(16, activation=tf.nn.relu),
    keras.layers.Dropout(0.5),
    keras.layers.Dense(1, activation=tf.nn.sigmoid)
])

dpt_model.compile(optimizer='adam',
                  loss='binary_crossentropy',
                  metrics=['accuracy','binary_crossentropy'])

dpt_model_history = dpt_model.fit(train_data, train_labels,
                                  epochs=20,
                                  batch_size=512,
                                  validation_data=(test_data, test_labels),
                                  verbose=2)

【結果】

Train on 25000 samples, validate on 25000 samples
Epoch 1/20
 - 5s - loss: 0.6502 - acc: 0.6037 - binary_crossentropy: 0.6502 - val_loss: 0.5363 - val_acc: 0.8463 - val_binary_crossentropy: 0.5363
Epoch 2/20
 - 4s - loss: 0.4932 - acc: 0.7775 - binary_crossentropy: 0.4932 - val_loss: 0.3655 - val_acc: 0.8794 - val_binary_crossentropy: 0.3655

＜中略＞

Epoch 19/20
 - 8s - loss: 0.1134 - acc: 0.9596 - binary_crossentropy: 0.1134 - val_loss: 0.4900 - val_acc: 0.8748 - val_binary_crossentropy: 0.4900
Epoch 20/20
 - 7s - loss: 0.1026 - acc: 0.9638 - binary_crossentropy: 0.1026 - val_loss: 0.5079 - val_acc: 0.8730 - val_binary_crossentropy: 0.5079

結果を表示します。

plot_history([('baseline', baseline_history), ('dropout', dpt_model_history)])

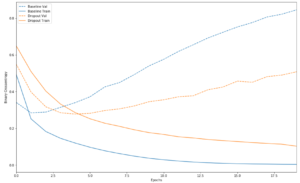
ドロップアウトを追加することでベースラインモデルを改善できました。

過剰適合を防ぐ最も一般的な方法

• より多くの訓練用データ
• ネットワークのキャパシティーを減らす
• 正規化を追加する
• ドロップアウトを追加する

上記以外に今回のチュートリアルで紹介されなかった２つの重要なアプローチがあります。それは、“データ増大”と、“バッチ正規化”です。